السقوط الشاقولي لجسم في مائع
القوى المطبقة على الجسم في حالة السقوط
كل جسم كتلته
m
يتحرك في مائع يخضع ل3 قوى:
قوة الثقل
قيمتها p=mg
حيث g
الجاذبية الأرضية.
تكون هذه القوة شاقولية متجهة نحو الأسفل
دافعة أرخميدس π
هي قوة شاقولية متجهة نحو الأعلى قيمتها
π=ρf×V×g
ρf: الكتلة الحجمية للمائع
V: حجم المائع المزاح يساوي حجم الجسم المدروس ب: m3
g: الجاذبية الأرضية ب: m/s2
قوة الإحتكاك مع المائع
هي قوة شاقولية معاكسة لجهة الحركة قيمتها
f=k×v
في حالة السرعات الصغيرة و
f=k×v2
في حالة السرعات الكبيرة حيث:
k
ثابت يتعلق بطبيعة المائع و أبعاد الجسم
المعادلة التفاضلية
بتطبيق القانون الثاني لنيوتن على الجسم الساقط نجد
المستوى: undefined undefined
الحصة: undefined
المجال: undefined
الوحدة: undefined
حالة السرعات الصغيرة
∑Fextp+π+fp−π−fmg−ρf×V×g−kvdtdvdtdv+mk×v=ma=maبعدالإسقاطعلىالمحورنجد:=ma=mdtdv=g−mρf×V×g−mk×v=g(1−mρf×V)
السرعة الحدية
VL=kmg(1−mρf×V)
حالة السرعات الكبيرة
dtdv+mk×v2=g(1−mρf×V)
السرعة الحدية
VL=kmg(1−mρf×V)
تطبيق 1 ★★★★☆
نضع داخل أنبوب زجاجي طوله
15cm
زيت كتلته الحجمية
ρf=0.92g/mL
نغمر كرية من الفولاذ في الزيت ثم نتركها بدون سرعة ابتدائية لتسقط شاقوليا
نعتبر قيمة قوة الإحتكاك المطبقة من طرف السائل على الكرية تعطى بالعبارة
f=kv
المستوى: undefined undefined
الحصة: undefined
المجال: undefined
الوحدة: undefined
- بتطبيق القانون الثاني لنيوتن برهن أن المعادلة التفاضلية لهذا السقوط تكتب على الشكل
dtdv=A−Bv
حيث
A و B
ثابتان.
- أحسب قيمة A
يمثل البيان التالي تغير السرعة للكرية بدلالة الزمن
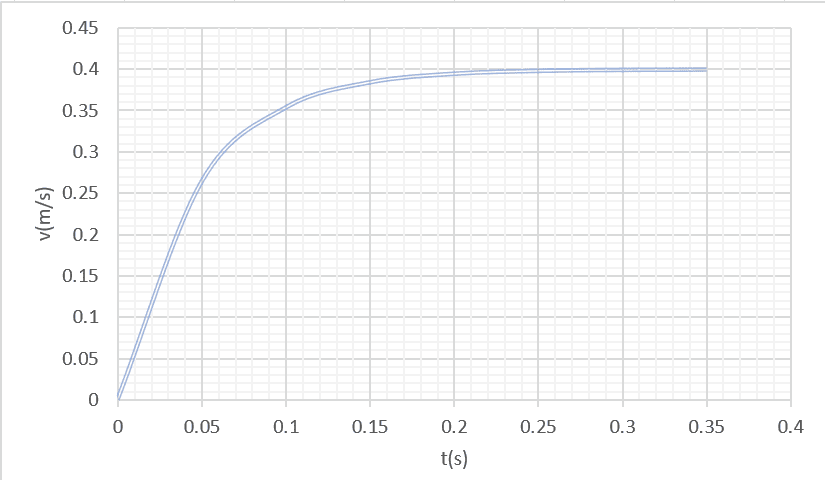
- عين بيانيا قيمة السرعة الحدية للكرية في الزيت
- أحسب قيمة الثابت B
معطيات:
الكتلة الحجمية للكرية الفولاذية
ρ=7.8g/mL
شدة الجاذبية الأرضية
g=9.8m/s2
تريد حل المزيد من التمارين؟