مبدأ العطالة

يحافظ كل جسم على سكونه أو حركته المستقيمة المنتظمة إذا لم تتدخل قوة لتغير حالته الحركية.

العلاقة بين شعاع تغير السرعة و القوة

لشعاع القوة نفس مميزات شعاع تغير السرعة أي:

لديهما نفس الجهة و المنحى, أما القيمة إذا كان شعاع تغير السرعة ثابت يكون شعاع القوة ثابت.

حساب السرعة اللحظية بيانيا

لحساب السرعة اللحظية بيانيا نستعمل المنحنى البياني للسرعة بدلالة الزمن و نتبع الخطوات حسب المثال التالي:

مثال: أحسب السرعة اللحظية $V_8$ باستعمال المنحنى البياني التالي:

يعطى: $\tau= 0.08s$

الخطوات	المثال
نحسب الزمن $t_8$ الخاص بالسرعة $V_8$	$t_8=\tau\times 8=0.08\times 8=0.64s$
نعين الزمن في محور الأزمنة ثم نقوم بالإسقاط على المنحنى بعد تمديده
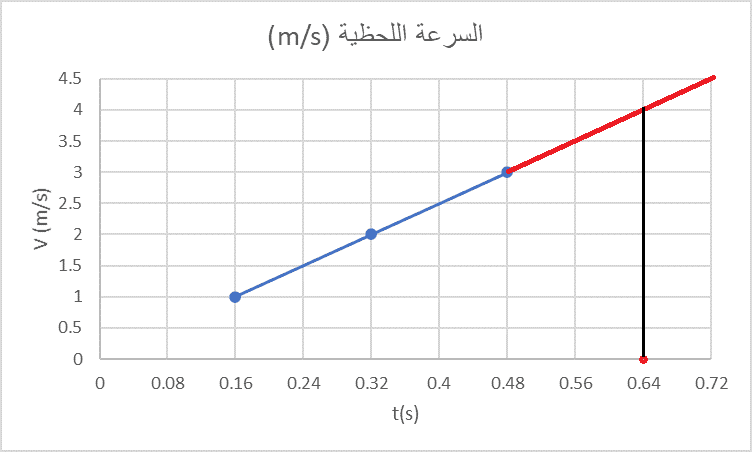
نسقط نقطة التقاطع على محور السرعات
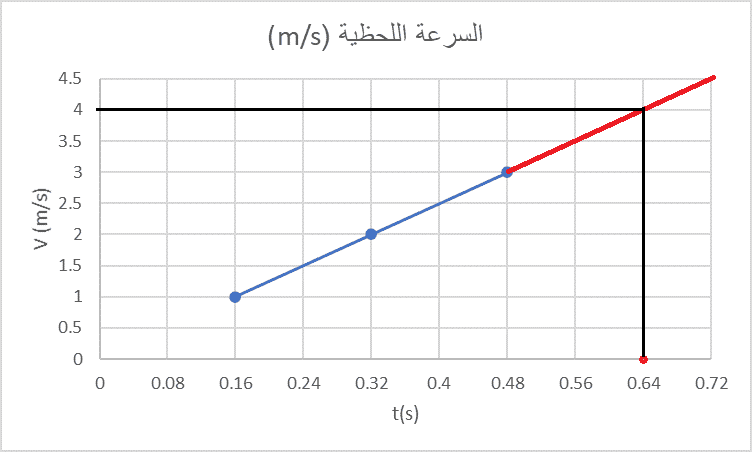
نعين السرعة بالقراءة المباشرة من المنحنى	$V_8 = 4 m/s$

حساب المسافة بيانيا

لحساب المسافة بيانيا يكفي إتباع خطوات المثال التالي:

المثال: باستعمال المنحنى البياني السابق أحسب المساف من الموضع $M_0$ إلى الموضع $M_5$

الخطوات	المثال
أسقط الزمنين الخاصين بالموضعين $M_0$ و $M_5$ على المنحنى
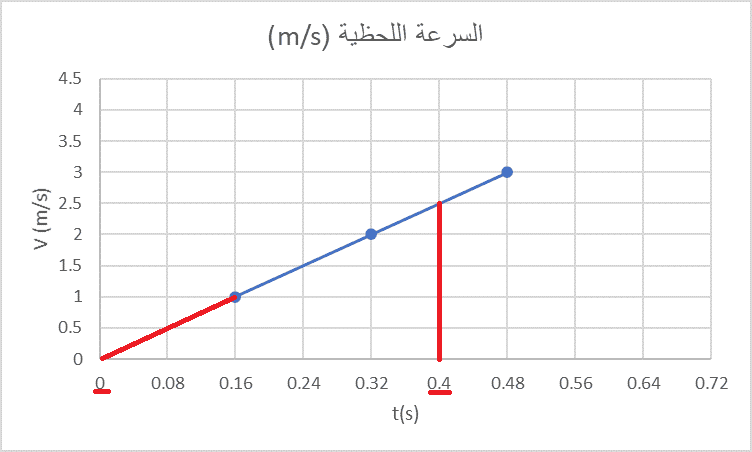
عين الشكل و قيم القاعدة والإرتفاع
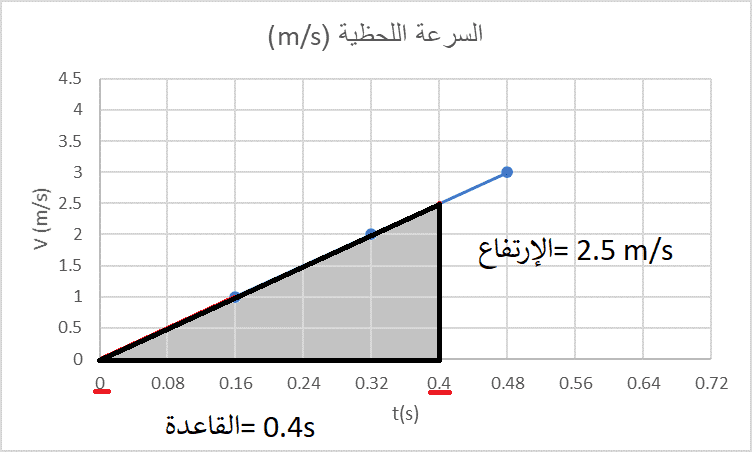
أحسب مساحة الشكل لتحصل على المسافة بالمتر	$M_0M_5=\frac{{القاعدة}\times{الإرتفاع}}{2}=2.5\times 0.4/2=0.5m$

تطبيق 1 ★★★★★

الجدول التالي يمثل سرعات جسم خلال حركته:

1. أرسم المنحنى البياني للسرعة بدلالة الزمن
2. أحسب سرعة الجسم عند الموضع $M_6$
3. أحسب المسافة بين الموضعين $M_0M_6$
4. هل هناك قوة مطبقة على الجسم, علل
5. ما هي مميزات شعاع القوة